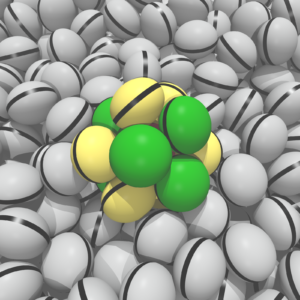
Kissing Ellipsoids
Ungeordnete Materialien wie Sand und Glas sind für Physiker schwieriger zu verstehen als gewöhnliche Kristalle. Die einzelnen Sandkörner ordnen sich in einer überwältigenden Vielzahl von lokalen Motiven an. In der Mathematik ist das lokale Packungsproblem von kugelförmigen „Sandkörnern“ gelöst worden: Die sogenannte Kusszahl ist zwölf, d.h. um ein Teilchen können maximal zwölf andere angeordnet werden, so dass alle Kontakt zum zentralen Korn haben. Eine besonders symmetrische Anordnung der zwölf Teilchen ist bekannt als „Ikosaedercluster“. Sogar dieses einfache Problem (ohne Schwerkraft) ist für asphärische Teilchen bisher ungelöst. Forscher der FAU haben nun die dichtesten Packungen ellipsoidförmiger Teilchen numerisch bestimmt und ihr Vorkommen als Bestandteile ungeordneter Ellipsoidpackungen untersucht. Die dichteste Packung wird dabei so bestimmt, dass das Set-Voronoi-Volumen um das zentrale Teilchen minimiert wird. So entsteht ein kompliziertes Optimierungsproblem, das numerisch gelöst werden kann. Je mehr die Ellipsoide von der Kugelform abweichen, desto höher ist die Packungsdichte im Zentrum, und desto mehr Nachbarteilchen finden um das Zentralteilchen Platz. Viele der dichtesten Strukturen weisen einen erstaunlich hohen Grad an Symmetrie auf. Weiterhin zeigt sich, dass die Verallgemeinerung des Ikosaederclusters in ungeordneten Packungen häufiger auftritt, als die bisherigen Theorien vorhersagen. Das vorgestellte Verfahren kann auf beliebig geformte und Mischungen verschieden geformter Teilchen übertragen werden, wie sie natürlicherweise in vielen Anwendungen z.B. in der Geologie oder in industriellen Prozessen vorkommen. Die Ergebnisse wurden kürzlich in der renommierten Fachzeitschrift Physical Review X veröffentlicht.
Weitere Informationen:
theorie1.physik.uni-erlangen.de
Dr. Sebastian Kapfer
Tel.: 09131/85-28448
sebastian.kapfer@fau.de